Une étape a été franchie !




Je me suis plongé dans le programme de Jean-Luc :
Une programmation objet avec polymorphisme, des récurrences et même des récurrences imbriquées…
Le résultat est un programme compact et efficace, mais, comme dire, … pas immédiat.

La place occupée en mémoire est limitée en deux temps :
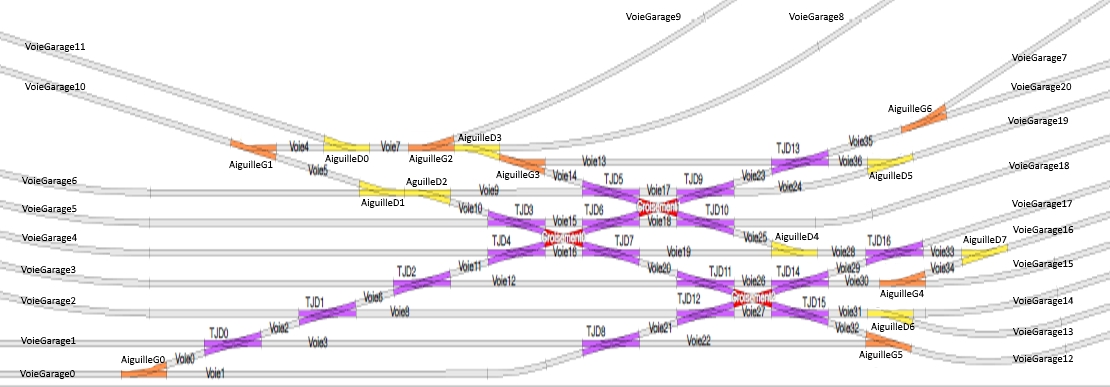
Dans le cas de ma gare, il y a 93 éléments :
- 8 aiguilles droites
- 7 aiguilles gauches
- 17 TJD
- 3 croisements
- 37 voies de liaison
- 21 voies de garage
Conseil d'ami : Je ne saurais trop vous conseiller d'imprimer le schéma des voies, sinon, vous allez avoir du mal à suivre les exemples.

Ils sont décris en seulement 12 octets (8 x 12 = 96) dans un "EnsembleDeVoies" et, en tenant compte du sens de déplacement, dans 24 octets (12 x 2) d'un "EnsembleDeVoiesOrientees".
Donc, au départ, Jean-Luc réserve par défaut 256 bits.
Puis, dans le enum{…}, on compte 93 éléments et via malloc et realloc, on le retaille à 96 bits dans la classe Voie(). On ne peut pas prendre moins de place.

Le classement dans le enum{…} n'est pas, ici, anodin. C'est lui qui va donner l'ordre d'affichage des éléments dans la description des itinéraires de Jean-Luc. J'expliquerai plus loin pourquoi je l'ai modifié.
Par manque de temps, ce programme n'a pas été terminé.
J'ai donc cherché à avancer, mais avec des méthodes moins sophistiquées, en utilisant les résultats du programme de Jean-Luc.
Il faut, en effet, ajouter deux notions fondamentales :1°) Donner l'orientation des aiguilles. C'est indispensable si on veut leur envoyer l'ordre d'aiguillage.


2°) Afficher les itinéraires dans l'ordre du parcours. Deux raisons à cela :
- Donner une note aux itinéraires pour savoir quel est le meilleur choix.
- Un peu moins nécessaire, mais ça fera plus joli quand on déclenchera les aiguilles les unes après les autres.
Si on suit bien le programme, on constate qu'à aucun moment la liste des itinéraires pour aller d'un point A à un point B n'est mémorisée.
Une seule ligne est calculée et mémorisée (c'est element[ i ]), affichée et effacée pour afficher la ligne suivante.
J'ai donc créé une matrice qui mémorise 15 itinéraires de 25 éléments, soit 375 bytes.
En faisant ça, j'ai eu l'impression de finir un lustre en cristal de Baccarat avec des pièces en plastique !


Pour information, le couple qui donne le plus grand nombre d'itinéraires est de VOIE_GARAGE_0 vers VOIE_GARAGE_16, avec 12 (!) solutions.
Et le plus grand, toujours pour ce couple, compte 21 éléments.
Ces deux informations expliquent la taille de la matrice.
Via malloc et realloc, je pourrais la retailler à 252 octets, mais ça n'est pas fait pour l'instant.
Cette fois, il va falloir conserver le numéro de l'élément et sa position pour les aiguilles, dans un seul byte.J'ai trouvé les principes suivants pour indexer 50 aiguilles et 100 voies (c'est déjà pas mal) :
1°) Je construis le enum{…] en commençant par les aiguilles. Je rappelle qu'il est généré automatiquement par le programme TCO en Processing.
Dans ma gare, 8 + 7 + 17 + 3 = 35, qui est bien < 50.
2°) Je mets les voies à la suite, en commençant donc à 36 jusqu'à 93.
Et 93 - 35 = 58 est bien < 100. On est donc dans les clous.
3°) Quand on sort d'une aiguille par la gauche, on ajoute 150 au numéro de l'élément
Quand on sort d'une aiguille par la droite, on ajoute 200 au numéro de l'élément.
Par exemple, la première aiguille gauche sera notée 9 quand on en sort par la pointe, 159 quand on en sort par la branche déviée et 209 quand on en sort par la voie directe.
On peut même indexer de cette façon les aiguilles triples, non traitées dans le programme jusqu'à maintenant.

Vous pourrez ainsi tester et vous verrez qu'aucun nombre n'est ambigu. Et vous voyez aussi pourquoi j'ai mis les aiguilles dans les 50 premiers dans le enum{...}.
Pour zéro, c'est vide dans l'impression.
Passons à l'analyse du programme de Jean-Luc :Avec 9 entrées pour 12 sorties, on s'attend à 9 x 12 = 108 itinéraires.
Comme il y en a 18 d'impossibles (ex VOIE_GARAGE_0 vers VOIE_GARAGE_9), il reste 90 couples origine - extrémité, chacun pouvant avoir plusieurs solutions.
Première bonne nouvelle :Pour chaque couple (parmi 90 couples), le "meilleur itinéraire" (voir post précédent) est le dernier de la liste. Hasard ?
Deuxième bonne nouvelle :Le meilleur itinéraire est le premier calculé ! Hasard ?
Vous avez tous été faire des courses dans un hyper et vous êtes forcément déjà tombé sur un caddie dont une roue est plus ou moins bloquée et vous tombez sur un "tourne à droite" ou un "tourne à gauche".
Et bien, le programme de Jean-Luc est un "tourne à droite" !Ce qui explique la deuxième bonne nouvelle, étant donné la définition du meilleur itinéraire.
Et aussi la première puisqu'ils sont affichés dans l'ordre inverse.
Je sens déjà poindre une objection : mais pourquoi une matrice, alors ?
Si tourner à droite est une bonne idée en allant de la gauche vers la droite, ce n'est pas forcément une bonne idée quand on va dans l'autre sens…
Et il me fallait comparer mes sorties avec celles de Jean-Luc.
Dernière raison : au moment où j'écris, je ne suis pas sûr que les bonnes nouvelles soient toujours vraies quand il faudra y intégrer les occupations de cantons. On verra.
Analyse du programme :Pour voir comment fonctionne le programme version Jean-Luc, il faut afficher, dans l'onglet Debug, DEBUG, TRACE et TRACE2.
Mais uniquement sur un seul couple A - B sous peine d'engorgement.
J'ai évidemment choisi VOIE_GARAGE_O vers VOIE_GARAGE_16 et ses 12 solutions.
On voit tout le déroulement, chaque élément choisi est affiché, avec une indentation croissante, que Jean-Luc appelle "profondeur" de l'itinéraire.
La première phase est donc simple : la profondeur va donner l'indice des colonnes dans la matrice.
Quand le cheminement arrive dans un cul de sac, le système repart du dernier de direction choix fait.
Et, donc, chaque nouveau cheminement efface l'ancien.
Voir le programme "GestionnaireReseau_JLB-DD_V2_1_AV_TR3.ino"
Pour être précis, deux choses sont à prendre en compte :1°) On n'efface pas tout depuis le début (surtout pas !), mais juste le nouveau cheminement.
2°) Il faut penser à changer la position des aiguilles quand on avance à nouveau.
Exemple du début :On part de la VOIE_GARAGE_0 et on finit VOIE_GARAGE_12. Il faut reculer.
On avait pris la VOIE_22 et, maintenant, on prendra la VOIE_21 qui va effacer la VOIE_22, puisque c'est la même profondeur (=> même colonne dans la matrice).
Mais TJD_8/D, vers la voie 22, donc doit devenir TJD_8/G vers la VOIE_21.
Ce qui se fait simplement en retirant 50 à TJD_8 qui vaut 24 au départ (d'après le enum{…}).
Il passe donc de 224 à 174.
Le cheminement bute ensuite sur l'AIGUILLE_G_50.
Pourquoi ? Ce n'est pas une voie de garage !?
Parce que ce programme démoniaque remarque qu'il est déjà passé par l'AIGUILLE_G_50 et que ça ne menait à rien !!

Le cheminement bute ensuite sur la VOIE_GARAGE_13, VOIE_GARAGE_14.
Là, on recule un grand coup jusqu'au CROISEMENT_2.
Puis on bute sur VOIE_GARAGE_15.
Et, enfin, via la VOIE_34, on arrive à VOIE_GARAGE_16.
Donc, les bons cheminements ont effacé petit à petit les mauvais choix et il a fallu modifier les orientations de TJD_8, TJD_12.
Normalement, on a fini, c'est le meilleur itinéraire.J'ai expliqué plus haut pourquoi on cherchait tous les itinéraires.
Et, là, ça se corse, comme disait Napoléon !
D'abord, il fallait trouver où la machine sortait les bons éléments, au fil de l'eau.
C'est au moment du marquage, dans chaque classe, là où j'ai ajouté mon traitement "noteAjoutBonneAiguille(0, sortie, profondeur, idVoie());", ligne 440 dans Voie.cpp.
0 : on va dans le sens gauche -> droite
sortie : donné une ligne au dessus. C'est là qu'on garde l'info de direction de sortie, elle même fonction du connecteur utilisé.
profondeur : indice de la colonne
idVoie() : indice de la voie
Il en faut un à chaque marquage et aussi quand on est arrivé au bout (ligne 433).
Maintenant que je vous l'ai expliqué, vous allez croire que c'était facile…
Et a suite ?C'est un peu plus loin, quand il y a "Serial.println(F("$$$$ Chemin partiel"));" (ligne 790).
Là, on ajoute une ligne dans la matrice par "ajouteItineraireMatrice();"
Il faut ajouter une ligne, mais elle ne va pas jusqu'au bout.
Pourquoi ?Parce qu'on arrive sur des éléments déjà visités.
Il va falloir compléter. Et avec quoi ?
Avec la fin de ligne qu'on a déjà créée !

En effet, on est maintenant avec un itinéraire déjà trouvé.
Il suffit de prendre l'élément terminal, là où on a bloqué, comme pivot.
Facile ! Et on continue…Que nenni !
Parce que maintenant, on a deux itinéraires complets et donc deux façons de terminer !
Dans le premier exemple, on a le choix en passant par la VOIE_29 et TJD_16 ou la VOIE_30 et AIGUILLE_G_40.
Donc, pour la VOIE_1, on a ces deux solutions (on vient de les construire).
Et, quand on va trouver via la VOIE_3, on va avoir ces deux solutions aussi.
En fait, on doit rechercher le pivot qu'on vient de trouver dans toutes les propositions précédentes pour ne pas oublier de possibilités de finir un début d'itinéraire.
Résumé jusqu'à présent :VOIE_1 … TJD_14/D VOIE_30 AIGUILLE_G_40/G VOIE_34 AIGUILLE_D_70/M VOIE_GARAGE_16
VOIE_1 … TJD_14/G VOIE_29 TJD_16/D VOIE_33 AIGUILLE_D_70/M VOIE_GARAGE_16
VOIE_3 … TJD_14/D VOIE_30 AIGUILLE_G_40/G VOIE_34 AIGUILLE_D_70/M VOIE_GARAGE_16
= début VOIE_3 + 1ere fin VOIE_1
VOIE_3 … TJD_14/G VOIE_29 TJD_16/D VOIE_33 AIGUILLE_D_70/M VOIE_GARAGE_16
= début VOIE_3 + 2eme fin VOIE_1
Et, si je continuais, j'aurais :
VOIE_3 … TJD_14/D VOIE_30 AIGUILLE_G_40/G VOIE_34 AIGUILLE_D_70/M VOIE_GARAGE_16
= début VOIE_3 + 1ere fin VOIE_3 !!
Mais on l'a déjà…
Et il faut donc l'effacer.
Cela se fait avec "ligneIdentique(byte ligneCourante)"
Quand je vous disais que ça n'était pas si facile que ça !
Et on remarquera que pour tous ces itinéraires, au début, on a deux solutions (VOIE_29 et VOIE_30) et puis, soudain, on a autre chose :
… VOIE_28 TJD16/D VOIE_33 AIGUILLE_D_7 VOIE_GARAGE_16.
Nous voilà maintenant avec 3 fins possibles.
Et voilà le résultat :
----------------------------------------------------------------------------------------------------------------------------------------------------------------
VOIE_GARAGE_0/M AIGUILLE_G_00/D VOIE_1/M TJD_8/G VOIE_21/M TJD_12/G CROISEMENT_2/G TJD_14/D VOIE_30/M AIGUILLE_G_40/G VOIE_34/M AIGUILLE_D_70/M VOIE_GARAGE_16/M
VOIE_GARAGE_0/M AIGUILLE_G_00/D VOIE_1/M TJD_8/G VOIE_21/M TJD_12/G CROISEMENT_2/G TJD_14/G VOIE_29/M TJD_16/D VOIE_33/M AIGUILLE_D_70/M VOIE_GARAGE_16/M
VOIE_GARAGE_0/M AIGUILLE_G_00/G VOIE_0/M TJD_0/D VOIE_3/M TJD_8/G VOIE_21/M TJD_12/G CROISEMENT_2/G TJD_14/D VOIE_30/M AIGUILLE_G_40/G VOIE_34/M AIGUILLE_D_70/M VOIE_GARAGE_16/M
VOIE_GARAGE_0/M AIGUILLE_G_00/G VOIE_0/M TJD_0/D VOIE_3/M TJD_8/G VOIE_21/M TJD_12/G CROISEMENT_2/G TJD_14/G VOIE_29/M TJD_16/D VOIE_33/M AIGUILLE_D_70/M VOIE_GARAGE_16/M
VOIE_GARAGE_0/M AIGUILLE_G_00/G VOIE_0/M TJD_0/G VOIE_2/M TJD_1/D VOIE_8/M TJD_12/G CROISEMENT_2/G TJD_14/D VOIE_30/M AIGUILLE_G_40/G VOIE_34/M AIGUILLE_D_70/M VOIE_GARAGE_16/M
VOIE_GARAGE_0/M AIGUILLE_G_00/G VOIE_0/M TJD_0/G VOIE_2/M TJD_1/D VOIE_8/M TJD_12/G CROISEMENT_2/G TJD_14/G VOIE_29/M TJD_16/D VOIE_33/M AIGUILLE_D_70/M VOIE_GARAGE_16/M
VOIE_GARAGE_0/M AIGUILLE_G_00/G VOIE_0/M TJD_0/G VOIE_2/M TJD_1/G VOIE_6/M TJD_2/D VOIE_12/M TJD_11/G VOIE_26/M TJD_14/D VOIE_30/M AIGUILLE_G_40/G VOIE_34/M AIGUILLE_D_70/M VOIE_GARAGE_16/M
VOIE_GARAGE_0/M AIGUILLE_G_00/G VOIE_0/M TJD_0/G VOIE_2/M TJD_1/G VOIE_6/M TJD_2/D VOIE_12/M TJD_11/G VOIE_26/M TJD_14/G VOIE_29/M TJD_16/D VOIE_33/M AIGUILLE_D_70/M VOIE_GARAGE_16/M
VOIE_GARAGE_0/M AIGUILLE_G_00/G VOIE_0/M TJD_0/G VOIE_2/M TJD_1/G VOIE_6/M TJD_2/G VOIE_11/M TJD_4/D VOIE_16/M TJD_7/D VOIE_20/M TJD_11/G VOIE_26/M TJD_14/D VOIE_30/M AIGUILLE_G_40/G VOIE_34/M AIGUILLE_D_70/M VOIE_GARAGE_16/M
VOIE_GARAGE_0/M AIGUILLE_G_00/G VOIE_0/M TJD_0/G VOIE_2/M TJD_1/G VOIE_6/M TJD_2/G VOIE_11/M TJD_4/D VOIE_16/M TJD_7/D VOIE_20/M TJD_11/G VOIE_26/M TJD_14/G VOIE_29/M TJD_16/D VOIE_33/M AIGUILLE_D_70/M VOIE_GARAGE_16/M
VOIE_GARAGE_0/M AIGUILLE_G_00/G VOIE_0/M TJD_0/G VOIE_2/M TJD_1/G VOIE_6/M TJD_2/G VOIE_11/M TJD_4/D VOIE_16/M TJD_7/G VOIE_19/M AIGUILLE_D_40/M VOIE_28/M TJD_16/D VOIE_33/M AIGUILLE_D_70/M VOIE_GARAGE_16/M
VOIE_GARAGE_0/M AIGUILLE_G_00/G VOIE_0/M TJD_0/G VOIE_2/M TJD_1/G VOIE_6/M TJD_2/G VOIE_11/M TJD_4/G CROISEMENT_0/G TJD_6/D VOIE_18/M TJD_10/D VOIE_25/M AIGUILLE_D_40/M VOIE_28/M TJD_16/D VOIE_33/M AIGUILLE_D_70/M VOIE_GARAGE_16/M
----------------------------------------------------------------------------------------------------------------------------------------------------------------Les 12 itinéraires y sont bien, dans l'ordre du calcul.
Ils sont décrits dans l'ordre de cheminement du train qui va les parcourir, en précisant, à chaque aiguille, si on sort par la gauche ou la droite !
Tout est prêt pour envoyer les ordres aux aiguilles !!
Mais on n'a pas fini.Si on teste sur tous les itinéraires (faites tourner GestionnaireReseau_JLB-DD_V2_3_AV_TR3.ino), on va trouver les 239 itinéraires de la gare…
Sur ces 239, seuls 90 sont utiles (il n'y a que 90 couples entrée-sortie). Dans le sens gauche vers droite. Parce qu'il y a aussi l'autre sens !
En fait, à priori, il y a 180 itinéraires utiles parmi les 239.
Fort bien. Mais j'entends déjà des réflexions …

Maintenant qu'on a trouvé les 90 meilleurs itinéraires, on pourrait se passer du programme et les affecter chacun à un bouton (méthode Märklin).
Outre le fait qu'il faudrait 180 (!!) boutons,
il reste un énorme problème :
Un wagon s'est détaché et reste sur la VOIE_1.
Si on a des itinéraires dont la définition est fixée une fois pour toutes, on ne peut plus aller de la VOIE_GARAGE_0 à la VOIE_GARAGE_16 !!
Et c'est là que l'affectation dynamique est formidable :
Un wagon décroché VOIE_1 ? Pas de problème : on va passer par la VOIE_3 !!
Mieux :Pour aller chercher ce fameux wagon, je ne vais pas demander VOIE_GARAGE_0 vers une autre voie de garage, comme on aurait dû le faire avec des itinéraires fixés.
Je vais demander VOIE_GARAGE_0 vers … VOIE_1, tout simplement.
Et, ainsi, TJD_8 pourra servir à un autre itinéraire. On pourra aller chercher ce wagon perdu sans désorganiser toute la gare.
C'est quand même souple, non ?
J'aimerais qu'un spécialiste d'un célèbre logiciel en version Silver ou Gold me dise comment ils gèrent ce cas.
Je vais vous laisser ingurgiter tout ça.
Et je suis sûr que, maintenant, vous penserez à Locoduino en poussant le caddie…



