Je propose aujourd'hui de faire le point sur ce que je veux faire, à terme, et ce qui fonctionne déjà.
Étant donné le prix des logiciels du commerce, n'ayant peur de rien, j'ai cherché à en faire un moi-même, à ma sauce.
Je dis tout de suite que, sans un site comme Locoduino, je n'y serais jamais arrivé. Imaginez qu'en 2014, je ne connaissais pas le langage C…
Quatre ordinateurs
Le premier, c'est celui du salon (ou du bureau, comme vous voulez) et vous devez installer dessus la dernière version de Java et du logiciel Processing.
Avec Processing, mon premier logiciel en Processing : TCO.
Processing ?Pour faire simple, un Arduino sait exécuter une tâche quand vous appuyez sur un bouton poussoir, allumer une LED, …
Mais il est très pauvre en entrées sorties avec un écran.
Processing sait, par contre, gérer quasiment tout ce que vous voulez faire sur un écran (faire tourner des figures en 3D, dessiner en 2D, …) mais il ne sait pas allumer une LED !
En fait, ces deux là sont faits pour s'entendre, via le bus série.
Donc, sur votre ordinateur (PC, Mac ou Linux) vous allez créer votre TCO en jouant avec des petits cubes. Vous pourrez les déplacer, les copier-coller ou couper-coller.
Tout ça avec une palette qui contient, à l'origine, tous les types de figures (ligne droite, courbe, aiguilles, croisements, TJD, TJS et triples)
J'ai voulu une interface sobre, épurée, avec le moins de texte possible.
En plus, je cherche à dessiner un réseau complet (c'est absolument indispensable ici, vous verrez pourquoi), une représentation assez proche de la réalité, y compris des longueurs à l'échelle.
On peut évidemment sauver le résultat et cela génère 4 fichiers textes :
Block___2016_11_10__08_04_55.tsv
C_panel_2016_11_10__08_04_55.tsv
Turnout_2016_11_10__08_04_55.tsv
Specifs.h
Les trois premiers sont liés par une date-heure commune (à la seconde près) et sont destines au deuxième ordinateur.
Le quatrième est destiné au troisième ordinateur.
Quand votre TCO est complètement dessiné, vous n'avez plus besoin du premier ordinateur. Après tout, on ne change pas de réseau tous les jours…
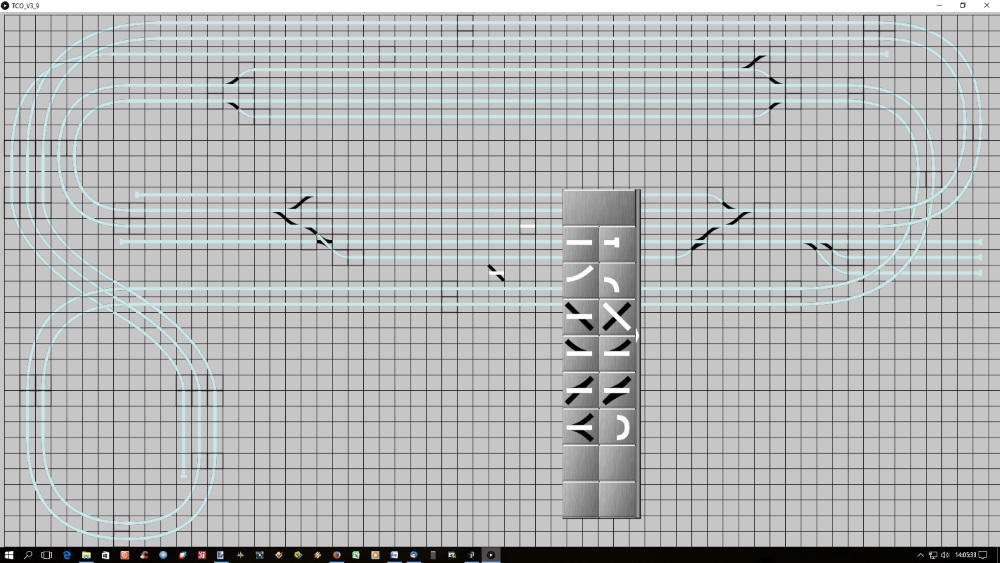 Le deuxième ordinateur
Le deuxième ordinateurCe n'est plus un vrai ordinateur, mais un couple PCDuino3 - écran.
Et quand je dis écran, c'est un grand écran (27", au moins) et il est attaché au mur, comme les vrais TCO.
Et si je pouvais, il ferait toute la longueur du mur, comme les vrais TCO.
Je pense qu'on peut même recycler une ancienne TV à écran plat.
PCDuino3 ?Pour 70 €, vous allez avoir un micro ordinateur qui fonctionne en Linux. L'écran se branche en HDMI.
Et comme Processing fonctionne aussi en Linux, vous installerez mon deuxième logiciel : Commandes.
Il faut copier les 3 fichiers en .tsv avec et vous retrouverez votre joli dessin de TCO, mais plus la palette qui servait à le dessiner.
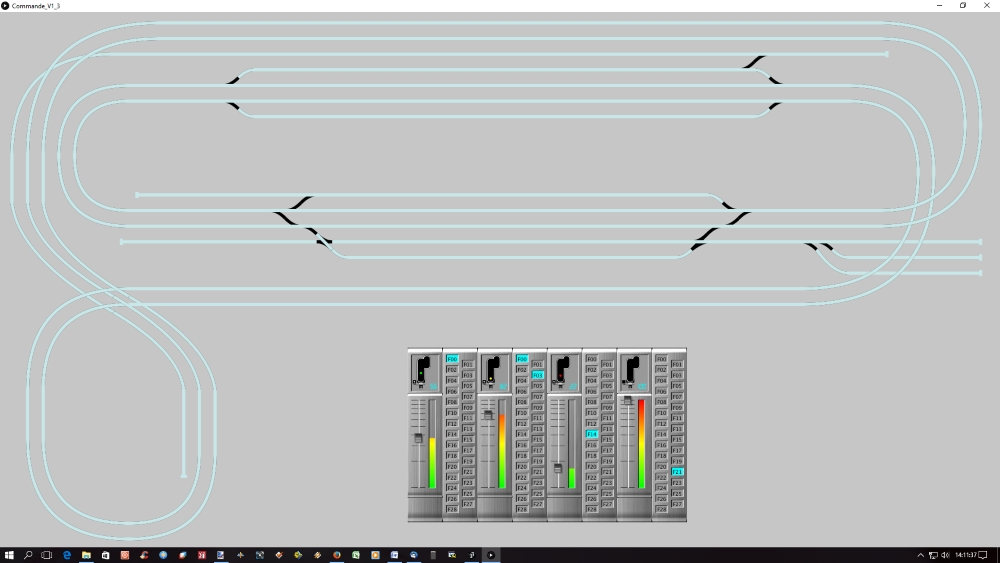
A la place, un boîtier de commandes qu'on peut déplacer et dimensionner pour conduire de 1 à n trains. Commande uniquement à la souris.
Cette partie est en cours de développement.
A court terme, je souhaite doter le programme de Jean-Luc d'entrées sorties plus conviviales en le gérant depuis Processing. Et intégrer le programme de Pierre (= Pierre59), celui qui gère le célèbre Locodrome.
Par rapport aux solutions du commerce, j'insiste sur trois points :1°) Maintenant que j'ai dessiné le TCO, je ne décrirai plus le réseau une nouvelle fois. Il faudra que ça se débrouille pour toutes les fonctions.
On vient de voir que le programme de Jean-Luc pouvait être intégré (
http://forum.locoduino.org/index.php?topic=167.45) et que donc, automatiquement, tous les itinéraires possibles sont calculés. C'est même tellement rapide qu'on n'a pas besoin de les sauvegarder : ils sont calculés à la demande, en quelques millisecondes.
Je ne veux pas non plus décrire des trajets : ce sera au programme de les trouver, en fonction de paramètres à définir.
2°) J'affiche sur chaque commande le signal que "voit" le conducteur de la loco.
Sous une forme agréable et conforme à la réalité SNCF, pas un simple voyant.
3°) Par ailleurs, je veux voir les trains se déplacer.
J'entends par "se déplacer" un mouvement continu. Pas un bond brutal de canton en canton.
Un mouvement coulé qui suit de belles courbes, sur des cantons pas forcément rectilignes, horizontaux ou verticaux.
C'est même cette fonction qui doit me permettre d'avoir sur la commande la vitesse réelle du train.
Quel plaisir de voir la vitesse réelle se rapprocher progressivement de la vitesse de consigne !
Certes, ça suppose que les paramètres DCC soient bien ajustés, via une phase de tests. A mon avis assez longue.
Donc, un point va se déplacer, accélérer, ralentir, en fonction de la vitesse réelle du train. C'est pour cette raison que le tracé du TCO doit correspondre au vrai tracé du train.
A chaque signal de changement de canton, d'aiguille, cela donnera un top qui resynchronisera le point par rapport au point sur l'écran. Plus les paramètres DCC seront précis, plus le dessin du TCO sera proche de la réalité, plus ce sera facile de resynchroniser.
Une fois qu'on est synchrone, tout est possible :
1°) Plus besoin de couper les rails pour les zones d'arrêt
2°) On peut déclencher une action (sifflet, par exemple) a un point précis du réseau, sans ILS ou autre.
Le troisième ordinateurCette fois-ci, c'est un Arduino DUE, gestionnaire du réseau.
Il est relié au PCDuino3 par un câble USB série (au moins pour les essais).
Il reçoit du PCDuino3 les ordres (choix d'itinéraires, vitesse, …) et lui envoie le résultat (occupation des cantons, couleur des signaux, …)
C'est là que vous utilisez le fichier "Specifs.h" généré par TCO, au début.
La partie description du réseau existe (le programme de Jean-Luc), mais il reste beaucoup à faire.
En particulier répondre à la question très complexe : parmi tous les itinéraires calculés, quel est le meilleur ?
C'est là aussi qu'il me faut intégrer la partie signaux de Pierre. J'ai bon espoir.
Et, évidemment, le DUE est relié au réseau via un bus CAN.
Je ne veux pas voir de fils sous le réseau.
Uniquement des câbles Ethernet avec des RJ11/RJ45 qui vont de modules en modules.
Jean-Luc a réalisé le premier d'entre eux : le module 8 aiguilles.
On fera évidemment un module cantons.
Les possibilités du bus CAN sont énormes et permettront à la fois de gérer la mise en place des aiguilles, mais de gérer aussi toute la rétro-signalisation.
Les bibliothèques de Thierry permettront une gestion simplifiée de tous ces échanges.
Le quatrième ordinateurC'est la centrale DCC, avec un Arduino MEGA.
Logiciel DCC++ dont Dominique vous a déjà parlé sur le Forum et dans des articles.
Relié bien sûr au gestionnaire. A définir.
Je penche pour un lien vers le DUE par le bus série et relier le DUE au PCDuino par un bus CAN.
Le deuxième bus CAN du DUE vers le réseau.
En fait, la seule information qui va être véhiculée sera du DUE vers le MEGA, c'est la vitesse maxi de consigne.
Exemple : "Je veux que le train 1 aille au maximum à 30 km/h".
Cela suppose que cette centrale DCC puisse commander plusieurs trains. A suivre.
Comme vous le voyez, c'est extrêmement ambitieux, mais faisable.
Et qu'on peut agglomérer les réalisations des uns et des autres en un ensemble complet.
C'est très motivant.
N'hésitez pas à vous exprimer, à donner vote avis.


